BAB III
DISTRIBUSI FREKUENSI
Distribusi
frekuensi adalah suatu cara meringkas dan menyusun sekelompok data mentah (row
data) yang diperoleh dari suatu pengukuran, dengan table frekuensi, sekelompok
data dapat dibaca dan dipahami dengan mudah. Ada dua jenis distribusi
frekuensi, yaitu : tunggal dan kelompok.
A.
Distribusi Frekuensi Tunggal
Distribusi tunggal
dicirikan dengan tidak adanya pengelompokan, nilai-nilai dari variable. Sebagai
contoh: seorang peneliti melakukan penelitian tentang, “tujuan mahasiswa
menghitung dengan metode jarimatika”. Dari 40 orang yang disurvei, didapat data
sebagai berikut.
Tabel
3.1. Frekuensi dan Persentase Tujuan Berolahraga
|
Tujuan Menggunakan metode jarimatika
|
Frekuensi
|
Persentase
|
|
(f)
|
(%)
|
|
|
Prestasi
|
10
|
25
|
|
Hobby
|
30
|
75
|
|
Total
|
40
= N
|
100
%
|
Rumus menghitung Persentase:
Jumlah kasus (n)
dibagi dengan jumlah total (N) dikalikan 100% , jika dirumuskan menjadi :
Dari data diatas,
kita juga dapat menghitung lebih jauh, misalnya mengenai proporsi dan rasio. Proporsi adalah perbandingan jumlah
kasus pada kategori tertentu dengan jumlah total, dengan menggunakan angka
dasar 1.
Dengan data diatas,
maka dapat dihitung proporsinya sebagai berikut :
Adapun rasio adalah perbandingan antara jumlah
kasus pada kategori tertentu dengan jumlah kasus pada kategori yang lain,
tergantung pada kategori apa yang ingin kita bandingkan, dengan menggunakan
angka dasar 1.
Dari contoh, dari
data pada table 2.1 diatas, maka rasio antara tujuan prestasi dan tujuan hobby
adalah sebagai berikut :
Angka
0,333 mengandung arti bahwa untuk satu orang yang berlatih menghitung dengan
metode jarimatika terdapat 0,333 yang bertujuan prestasi. Untuk mempermudah
pemahaman, angka decimal tersebut bisa dibulatkan dengan mengalikan dengan
angka 100. Dengan demikian didapatkan rasio 33, Artinya dalam setiap 100 orang
yang berlatih terdapat 33 orang yang belajar berhitung dengan metode jarimatika
untuk tujuan olahraga. Dengan kata lain rasio antara tujuan prestasi dan tujuan
hobby adalah 10:30 = 1:3
- Distribusi Frekuensi Kelompok
Distribusi Frekuensi
Kelompok dicirikan oleh penggunaan kelas interval untuk menggambarkan nilai
dari variable. Penggunaan interval dalam frekuensi kelompok dikarenakan
angka-angka hasil pengukuran sangat heterogen, yang tidak dapat dikelompokkan
dan disimbolkan oleh satu jenis angka tertentu sebagaimana dalam distribusi
tunggal.
Sebagai contoh,
seorang guru IPA memberikan nilai kepada 40 muridnya dengan variasi skor sbrk:
50 56 59 65 65 66 68 68
70 70 70 75 75 75 76 76
76 76 77 78 78 78 78 79
79 80 80 80 82 82 85 85
85 85 86 86 88 88 88 90
Bagaimana membuat distribusi frekuensi dari
skor-skor tersebut?
Langkah-langkah Penyelesaian :
1. Temukan skor tertinggi dan skor terendah.
Dalam data diatas skor tertinggi adalah 90 dan skor terendah adalah 50.
2. Temukan range (jarak pengukuran), yaitu (skor
tertinggi – skor terendah) + 1.
Range
=(90-50) + 1 = 41
3. Tetapkan nilai kelas interval, berkisar antara 5 sd 15. (usahakan
jumlah kelas interval dalam bilangan ganjil agar mudah ditentukan kelompok
tengahnya.)
Jumla kelas interval = 5.
4. Hitung lebar interval, yaitu range dibagi jumlah kelas interval
Lebar interval = 41/5 = 8, 2
≈ 9
5. Susun kelompok-kelompok interval ke dalam table dengan
memperhatikan hasil perhitungan yang telah dilakukan.
Tabel 3.2. Dsitribusi Frekuensi Nilai IPA dari
40 Siswa
Skor 86, 77, 68, 59 dan 50
dalam kelas interval di atas disebut batas bawah; sedangkan skor 94, 85, 76, 67
dan 58 disebut batas atas. Kedua batas tersebut pada dasarnya merupakan batas semu, mengapa? Karena kedua batas
tersebut tidak dapat menghubungkan antara kelompok interval yang satu dengan
yang lainnya. Sebagai gambaran lihatlah ilustrasi berikut:
58,5 67,5
76,5 85,5
Dalam
contoh tersebut diatas skor 85,5 disebut batas
nyata.
Latihan
Soal untuk didiskusikan dalam kelompok:
Buatlah
distribusi frekuensi untuk kelompok data beriku, lakukan langkah-langkah sesuai
petunjuk di atas).
12 9 12 13 10
19 15 15 10 14
16 14 13 20 12
17 9 14 17 15
BAB IV
PENYAJIAN DATA
Data statistika tidak hanya cukup dikumpulkan dan diolah, tetapi juga
perlu disajikan dalam bentuk yang mudah dibaca dan dimengerti oleh pengambil
keputusan. Penyajian data dalam bentuk diagram meliputi: Diagram Batang,
Diagram Lingkaran, Diagram Lambang, Diagram Garis, Diagram Pastel, Diagram
Grafik, Diagram Table/Daftar.
Sebuah grafik yang lengkap pada umumnya terdiri dari 13 bagian. Ketiga
belas bagian dimaksud adalah:
a. Nomor grafik
- Judul grafik
- Sub-judul grafik
- Unit skala grafik
- Angka skala grafik
- Tanda skala grafik
- Ordinat atau ordinal atau sumbu vertical.
- Koordinat (garis-garis pertolongan =
garis kisi-kisi).
- Abscis (sumbu horizontal = sumbu mendatar
= Garis Nol = Garis awal = Garis Mula.)
- Titik nol (titik awal)
- Lukisan grafik (Gambar Grafik)
- Kunci grafik (keterangan grafik)
- sumber Grafik (sumber data)
A. Model Penyajian Data
1. Diagram Batangan.
Diagram
batang adalah diagram berdasarkan data berbentuk kategori. Diagram ini banyak
digunakan untuk membandingkan data maupun menunjukkan hubungan suatu data
dengan data keseluruhan. Diagram ini penyajian datanya dalam bentuk batang,
sebuah batang melukiskan jumlah tertentu dari data.
Contoh :
sumber data dari table 3.1
Gambar
Batang Frekuensi dari Tabel 2.1
Tujuan
Mahasiswa Berhitung dengan metode
jarimatika
Langkah-langkah
dasar pembuatan diagram batang adalah sebagai berikut :
- Buat sumbu mendatar dan sumbu tegak yang
saling tegak lurus.
- Sumbu mendatar dibagi menjadi beberapa
skala bagian yang sama, demikian pula sumbu tegaknya: Skala pada sumbu
mendatar dengan skala pada sumbu tegak tidak perlu sama.
- Jika diagram batang dibuat tegak, maka
sumbu mendatar menyatakan keterangan atau fakta mengenai kejadian
(peristiwa). Sumbu tegak menyatakan frekuensi keterangan.
- Jika diagram batang dibuat secara
Horisontal, maka sumbu tegak menyatakan keterangan atau fakta mengenai
peristiwa. Sumbu mendatar menyatakan frekuensi keterangan.
- Tunjukkkan 1 batang untuk mewakili
frekuensi data tertentu.
- Arsir batang yang memenuhi frekuensi data
- Beri judul diagram batang.
- Variasi diagram batang, dapat dibuat
sesuai keahlian guru.
2. Diagram Lingkaran
Penyajian data dalam bentuk diagram
Lingkaran didasarkan pada sebuah lingkaran yang dibagi-bagi dalam beberapa
bagian dengan macam data dan perbandingan frekuensi masing-masing data yang
disajikan.
Contoh :
Langkah-langkah dalam membuat diagram lingkaran adalah sebagai berikut
:
- Ubah nilai data absolute ke dalam bentuk
persentase untuk masing-masing data.
- Tentukan juring sudut dari masing-masing data yang ada denga rumus :
- Buat sebuah lingkaran dengan menggunakan
jangka, ukuran lingkaran jangan terlalu besar dan jangan terlalu kecil.
- Masukkan data yang pertama dengan
menggunakan busur derajat dimulai dari titik tertinggi.
- Masukkan data-data lainnya ke dalam
lingkaran sesuai juring sudut data yang telah dihitung searah jarum jam
- Setiap data yang terdapat dalam
lingkaran, hendaknya diberi arsir atau warna yang berbeda.
- Masing-masing data yang terdapat dalam
lingkaran diberi Identitas :
a. Nama data disertai nilai persentasenya, atau
b. Nilai persentasenya saja, sedangkan nama data
dicantumkan pada catatan tersendiri yang terletak diluar lingkaran disertai
dengan arsir atau warna yang sesuai seperti yang terdapat di dalam lingkaran.
3. Diagram Gambar (Lambang)
Diagram gambar sering dipakai untuk memperoleh gambaran kasar sesuatu
peristiwa. Pada diagram ini sebuah gambar mewakili jumlah tertentu dari data.
Lambang yang digunakan harus sesuai dengan objek yang diteliti. Misalnya data
yang digunakan mengenai sejumlah siswa, maka lambing yang digunakan adalah
gambar orang. Kesulitan yang sering dihadapi ialah ketika menggambarkan bagian
gambar yang tidak sesuai dngan wakil gambar untuk jumlah tertentu.
Contoh:
Jumlah
siswa SD Pemuar Tahun 1990
|
Kelas
|
Jumlah SIswa
|
Frekuensi
|
|
Satu
|
☺
|
30
|
|
Dua
|
☺☺
|
40
|
|
Tiga
|
☺☺☺
|
40
|
|
Empat
|
☺☺☺☺
|
50
|
|
Lima
|
☺☺☺☺☺
|
40
|
|
Enam
|
☺☺☺☺☺☺
|
50
|
☺ mewakili 10 siswa.
Langkah-langkah dalam membuat diagram lambing adalah sebagai berikut.
1. Buatlah tiga buah kolom, dengan ketentuan
sebagai berikut :
a. Kolom
pertama berisi nama data/kategori
b. Kolom
kedua beris lambang yang digunakan
c. Kolom
ketiga berisi frekuensinya
2. Di bawah diagram diberi catatan berisi satu
lambing yang mewakili sejumlah objek tertentu.
3. Tulis nama kategori pada kolom, gambarkan
lambangnya pada kolom lambang dan tuliskan banyak datanya pada kolom
frekuensinya.
4. Banyak lambang yang digambarkan tidak sama
dengan banyak yang ada
5. Untuk kategori lainnya dapat dilakukan seperti
kategori yang pertama.
4. Diagram Garis
Diagram garis adalah suatu diagram yang
digambarkan berdasarkan satu waktu, biasanya waktu yang digunakan dalam bulan
atau tahun. Kegunaan diagram garis adalah untuk dapat melihat gambaran tentang
perubahan peristiwa dalam suatu periode (jangka waktu) tertentu dibuat diagram
garis.
Contoh :
Langkah-langkah dalam membuat diagram garis
adalah sebagai berikut :
a. Untuk menggambar diagram garis yang diperlukan
sumbu mendatar dan sumbu tegak yang saling tegak lurus.
b. Sumbu mendatar biasanya menyatakan waktu,
sedangkan frekuensi tegak menyatakan
frekuensi data.
c. Dalam pembagian skala masing-masing sumbu
tidak menggunakan skala yang sama
d. Gambar titik sesuai waktu dan frekuensi data
e. Jika semua data sudah disesuaikan pada
masing-masing sumbu, maka akan terdapat sekumpulan titik-titik
f. Hubungkan titik-titik yang ada sehingga
diperleh suatu kurva.
Latihan : Memilih Diagram yang Tepat
Jika ada sejumlah data dan akan disajikan
dalam bentuk diagram, bagaimanakah memilih diagram cocok untuk menyampaikan ide
tersebut?
Gunakan data dibawah ini.
Kasus
penganiayaan yang ditangani oleh RSUD dr. Sutomo.
|
Tahun
|
Banyaknya
|
|
1998
|
1184
|
|
1999
|
1050
|
|
2000
|
916
|
Sumber. Jawa Pos
Manakah diagram di bawah ini yang sesuai
dengan data tersebut ? kemudian gambarlah diagram yang menurut Anda paling
sesuai.
1. Diagram Batang
2. Diagram Garis
3. Diagram Lingkaran
Jelaskan jawaban Anda.


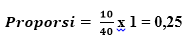






Tidak ada komentar:
Posting Komentar